확률 이론은 통계 분석과 머신 러닝의 핵심입니다. 데이터 과학자로서 견고한 모델을 이해하고 개발하는 데 이를 숙달하는 것이 중요합니다. 이 블로그에서는 확률 이론의 주요 개념을 소개하며, 집합 이론의 기초부터 고급 베이지안 추론까지 상세한 설명과 실제 예제로 안내해 드릴 것입니다.

목차

• 소개
• 기본 집합 이론
• 기본 확률 개념
• 확률 변수와 기대값
• 주변, 결합 및 조건부 확률
• 확률 규칙: 주변화 및 곱셈
• 베이즈 정리
• 확률 분포
• 학습을 위한 확률 활용
• 베이지안 추론
• Python에서 확률 개념 구현
• 장난감 예제: 동전 던지기에 대한 베이지안 추론
• 결론
• 행동 요청

소개

확률 이론은 불확실성을 양적화하기 위한 수학적 프레임워크입니다. 우리에게 무작위 현상을 모델링하고 분석할 수 있게 해주며, 통계학, 기계 학습 및 데이터 과학에서 필수적입니다. 확률 이론은 우리에게 정보를 기반으로 한 결정을 내릴 수 있게 해주고, 위험을 평가하고 예측 모델을 구축하는 데 도움을 줍니다.

기본 집합 이론

먼저 몇 가지 주요 용어를 정의해 봅시다.

집합(Set)은 객체의 모음입니다. 이 객체들은 집합의 요소(elements)라고 불립니다.

집합 a의 부분집합 b는 a의 요소인 요소들로 이루어진 집합입니다, 즉 b ⊂ a입니다.

공간 S는 가장 큰 집합이며, 따라서 모든 다른 집합들은 고려 대상에 포함됩니다 𝑠ᵢ ⊂ 𝑆.

공집합 O는 요소가 없는 빈 집합이거나 널 집합입니다. O는 요소를 포함하지 않습니다.

집합 이론의 구성 요소를 시각화해 봅시다.

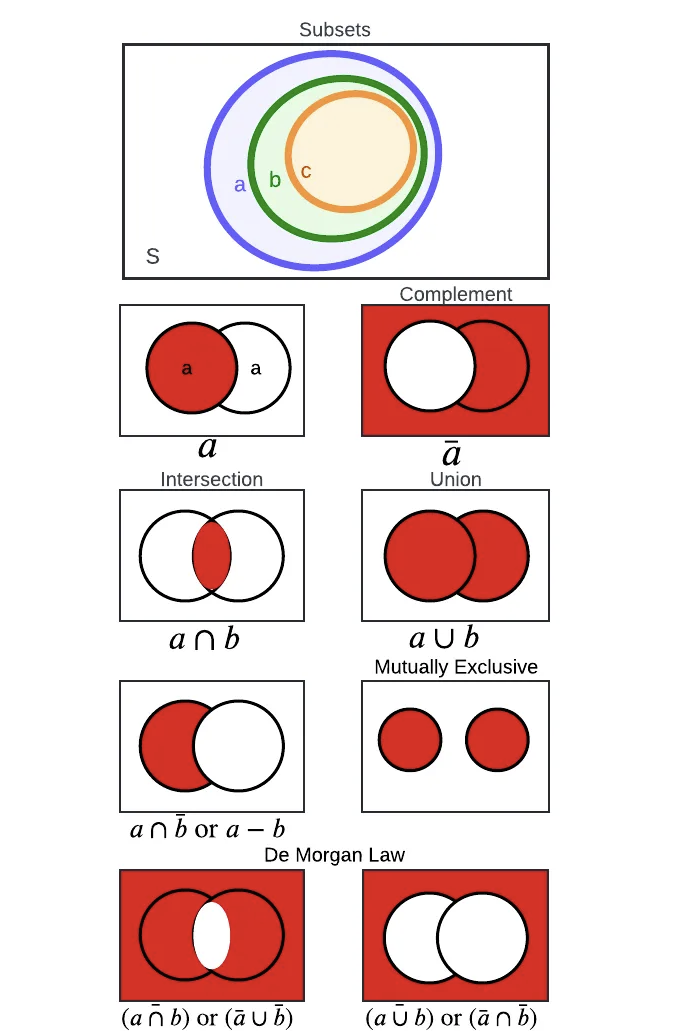
Subsets

Subset 𝑏 ⊂ 𝑎, or the set a contains b, 𝑎 ⊃ 𝑏 if all elements of b are also elements of a. That is,

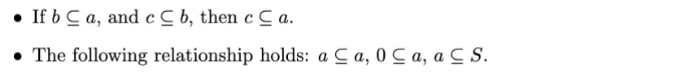
영어: "b ⊆ a이고, c ⊆ b이면, c ⊆ a"라는 명제는 집합 포함성의 추이성을 나타냅니다. 만일 집합 b가 집합 a의 부분집합이고, 집합 c가 집합 b의 부분집합이라면, c는 반드시 a의 부분집합이어야 합니다. 두 번째 항목 "다음 관계가 성립한다: a ⊆ a, ∅ ⊆ a, a ⊆ S"는 집합 포함성의 기본 속성을 강조합니다. 따라서:

• a ⊆ a는 모든 집합이 자신의 부분집합임을 나타냅니다.
• ∅ ⊆ a는 빈 집합이 어떤 집합 a의 부분집합임을 나타냅니다.
• a ⊆ S는 모든 집합 a가 전체 집합 S의 부분집합임을 나타냅니다.

집합 연산

동등성: 두 집합이 동일하려면 a의 모든 요소가 b에 있어야 하며, b의 모든 구성요소가 a에 있어야 합니다. 수학적인 용어로 표현하면:

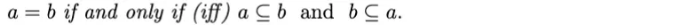
합집합 (합): 두 집합 a와 b의 합집합은 a 또는 b 또는 둘 다의 모든 요소로 이루어진 집합입니다. 합집합 연산은 다음 속성을 만족시킵니다:

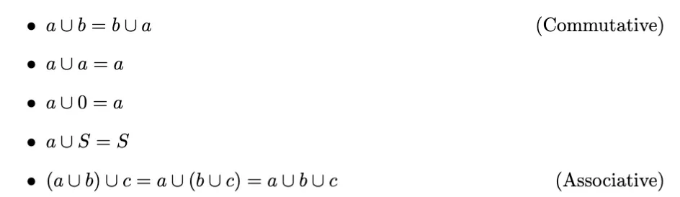
집합 a와 b의 교집합은 집합 a와 b의 모든 공통 요소로 구성됩니다. 교집합 연산은 다음과 같은 속성을 만족합니다:

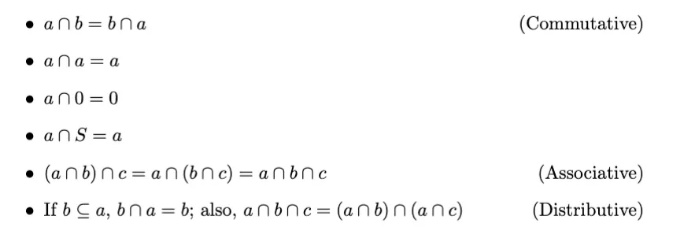
상호 배타적인 집합

만일 두 집합 a와 b가 어떤 공통 요소도 없는 경우, 즉 함께 존재하지 않는 경우, 우리는 두 집합을 상호 배타적이거나 서로소라고 부릅니다.

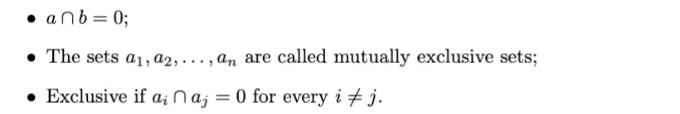
보완

집합 a의 역은 집합 a에 포함되지 않는 S의 모든 요소로 구성된 집합으로 정의됩니다. 역집합은 다음과 같은 특성을 만족합니다:

De Morgan Law

이 이미지는 집합 이론과 불 대수에서 기본 규칙인 De Morgan의 법칙을 설명합니다. 이 법칙은 집합의 합집합, 교집합 및 여집합 간의 관골 관계를 설명합니다.

두 집합의 차집합

a - b의 차집합은 b에 없는 a의 요소들의 집합입니다. 이 차집합은 다음 속성을 만족합니다:

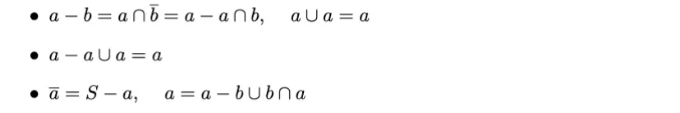
Basic Probability Concepts

Sample Space (S): The set of all possible outcomes of a random experiment.

Event (E): A subset of the sample space comprising a specific outcome or a set of outcomes.

랜덤 변수 (RV): 무작위 현상의 수치적 결과로 가능한 값을 가지는 변수. 예시: 사람의 키, 동전 던지기나 주사위 굴리기의 결과.

사건의 확률

사건 E의 확률 (즉, P(E))은 해당 사건이 발생할 가능성을 측정한 것입니다. 다음과 같은 특성을 충족합니다:

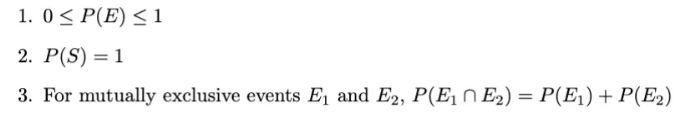
예시

공정한 여섯 면 주사위를 고려해 봅시다. 표본 공간은 S = '1, 2, 3, 4, 5, 6' 입니다. 3이 나올 확률은 P('3') = 1/6 입니다. 그렇다면 1 또는 3이 나올 확률은 어떨까요? P('1, 3') = 2/6 = 1/3 입니다. 마지막으로, 짝수가 나올 확률은 어떨까요? P('2, 4, 6') = 3/6 = 1/2 입니다.

랜덤 변수와 기대값

이 부분에서는 합과 적분을 사용합니다. 미적분 및 선형 대수에 대해 다루는 이 시리즈의 이전 부분을 참고해 주세요.

무작위 변수 (RV)

RV(무작위 변수)는 결과에 따라 값이 결정되는 변수입니다. 두 가지 유형이 있습니다: 이산형 무작위 변수는 카운트 가능한 수의 값을 가지며 연속형 무작위 변수는 계수 불가능한 수의 값을 가집니다.

예를 들어, 이산형 무작위 변수의 분포:

• 각 값이 발생할 확률.
• 표기법: P(X = xi).
• 이러한 숫자는 다음을 충족합니다:

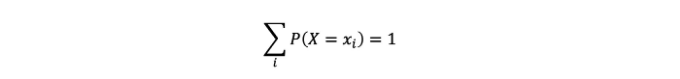
기대값과 분산

기대값 (평균): 랜덤 변수의 평균값을 의미합니다.

• 이산형 랜덤 변수의 경우:

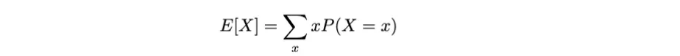
이 기대값(즉, 평균)은 이산 확률 변수 X입니다. 따라서 가능한 모든 값 x에 대한 확률 P(X = x)로 가중치를 곱한 값의 합으로 계산됩니다.

• 연속 확률 변수의 경우:

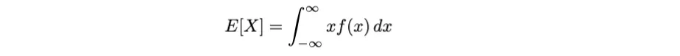
이 기대값(즉, 평균)은 연속 확률 변수 X의 것입니다. 우리는 x를 그 확률 밀도 함수 f(x)로 곱한 후 가능한 값의 전체 범위에 걸쳐 적분하여 계산합니다.

요약하면:

분산: 우리는 기대값으로부터 확률 변수의 퍼짐 정도를 나타내는 2차 통계적 측정을 계산할 수 있습니다.

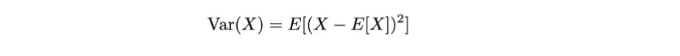
The above equation represents the variance of a random variable X, measuring its spread or dispersion of the values of X around its mean E[X].

Example

For a fair six-sided die, the expected value is:

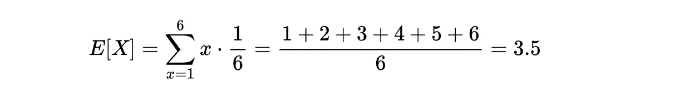
주변, 결합, 조건부 확률

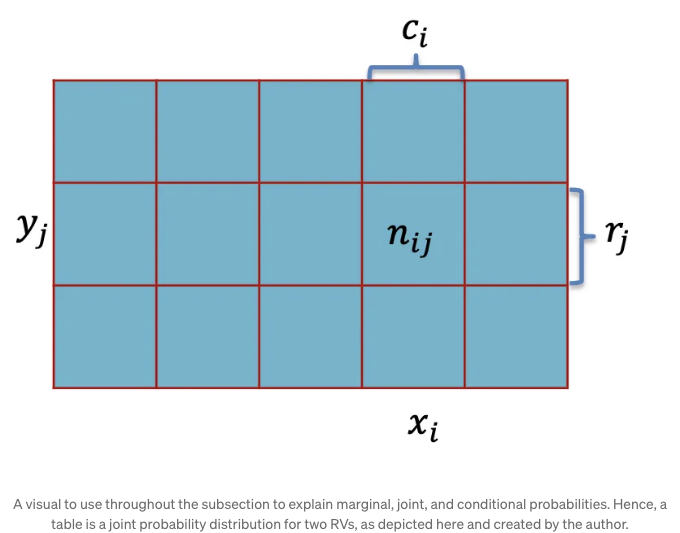
위의 이미지를 살펴보세요. 우리는 이 시각 자료를 사용하여 확률 이론에서의 기본 개념인 주변, 결합 및 조건부 확률을 배우게 됩니다. 이러한 개념들은 랜덤 변수간의 관계를 이해하는 데 중요하며, 특히 범주형 또는 계수 자료를 다룰 때 유용합니다.

주변 확률

주변 확률은 다른 사건을 고려하지 않고 단일 사건이 발생할 확률을 의미합니다. 이미지에서 p(X = xᵢ)로 표시됩니다. 그런 다음 다음과 같이 계산합니다:

이는 확률 변수 X가 특정 값을 xᵢ로 취하는 확률을 나타내며, 다른 변수들의 모든 가능한 값들에 대해 주변화된 것입니다. 따라서 다른 변수의 모든 가능한 결과와 함께 해당 이벤트의 공동 확률을 합산하여 한 사건의 확률을 찾는 데 도움이 됩니다.

결합 확률

결합 확률은 두 이벤트가 동시에 발생할 확률을 나타냅니다. 위의 이미지를 참조하면, 이는 확률 p(X = xᵢ, Y = yⱼ)로 계산됩니다.

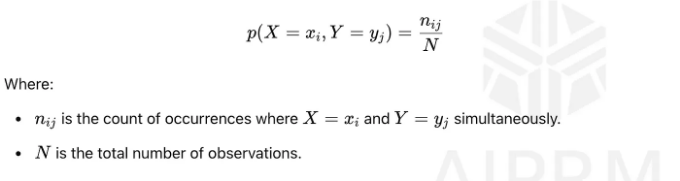
이 결합 확률은 이벤트 X = xᵢ와 Y = yⱼ가 함께 발생할 가능성을 측정합니다.

조건부 확률

조건부 확률은 다른 이벤트가 이미 발생했을 때 어떤 이벤트가 발생할 확률을 측정합니다. 위 이미지는 p(Y = yⱼ | X = xᵢ)로 정의되며, 다음과 같이 계산됩니다:

이 공식은 X = xᵢ가 이미 발생했을 때 Y = yⱼ가 발생할 확률을 보여줍니다.

확률 규칙: 마진ㅣㅑ제화와 곱셈

마진ㅣㅑ제화는 확률 이론에서 모든 변수의 결합 확률 분포로부터 일부 변수와 관련된 이벤트의 확률을 도출하는 데 사용되는 과정입니다.

이 방정식에서는 다른 변수 Y의 모든 가능한 값들을 합함으로써 주변 확률 p(X = xᵢ)를 계산합니다:

제품 규칙(Product Rule)은 확률에서 두 사건의 결합 확률을 그들의 주변 확률(marginal probability) 및 조건부 확률(conditional probability)로 표현할 수 있게 해주는 기본 개념입니다.

이 방정식은 두 개의 사건의 결합 확률 p(X = xᵢ, Y = yⱼ)을 분해하는 방법을 보여줍니다:

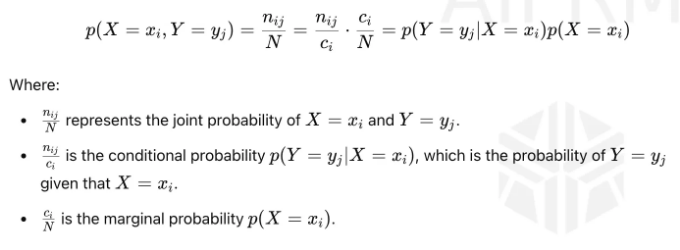
구체적으로, 수학적으로 표현하면, 제품 규칙은 한 사건의 주변 확률과 다른 사건의 조건부 확률을 사용하여 두 사건의 결합 확률을 계산할 수 있게 해줍니다.

요약

이러한 개념들은 확률 이론에서 기본적이며, 데이터 과학에서 더 복잡한 확률 모형 및 추론 기술을 이해하는 데 중요합니다. 아래에 설명을 제공합니다.

마지막으로, 𝑋와 𝑌가 독립이면 P(Y | X) = P(Y)이며, 이는 P(𝑋, 𝑌) = P(X)P(Y)임을 의미합니다.

베이즈 이론

베이즈 이론, 베이지안 추론의 기초,는 우리가 이전에 알고 있던 정보를 계산에 반영할 수 있도록 해주는 강력한 확률적 구조입니다.

조건부 확률로 돌아가서 그것을 바탕으로 확장해보겠습니다: 우리는 이전에 p(Y = yⱼ | X = xᵢ)를 정의했었습니다. 이를 사건 A와 B를 활용하여 일반화할 수 있는데, 우리는 이를 더 발전시켜 베이즈의 이론으로 확장할 것입니다.

따라서, 조건부 확률은 다른 사건이 발생했을 때의 사건의 확률을 양적으로 표현합니다. 따라서, 사건 A가 발생했을 때 사건 B가 발생할 확률은 A와 B의 결합 확률을 B의 확률로 나눈 비율입니다. 이를 P(A | B)로 표기하고 다음과 같이 정의합니다:

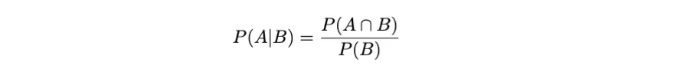
확률 이론에서는 파이프 문자 "|"이 "주어진"을 의미합니다.

그러므로 베이즈 정리는 두 이벤트의 조건부 확률을 다음과 같이 관련시킵니다:

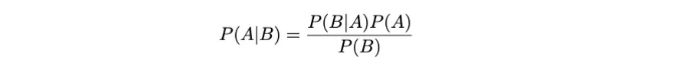
이 용어는 우도 P(B | A), 사전확률 P(A), 및 주변 확률 P(B)을 이용하여 조건부 확률 P(A | B)를 표현합니다. 다시 말해서, 이 구조는 베이지안 추론에서 기본적인 역할을 하며, 새로운 증거에 기반하여 우리의 믿음을 업데이트할 수 있도록 합니다.

예시

다음과 같은 확률을 갖는 질병을 진단하는 테스트가 있다고 가정해 봅시다:

Bayes' 이론을 사용하여 P(질병|양성)을 찾을 수 있습니다:

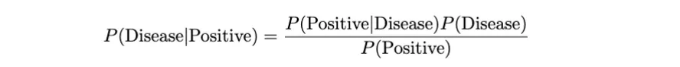
여기서 P(양성)을 계산할 수 있습니다:

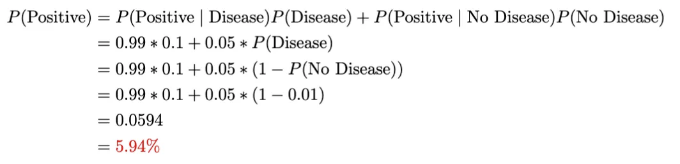
해당 방정식은 질병을 가지고 있는지 여부를 고려하여 양성 판정 확률의 총합을 나타냅니다: 총확률의 법칙의 직접 적용입니다.

확률 분포

전형적인 추세는 알려진 분포를 따릅니다. 따라서, 흔한 문제는 우리의 데이터에 맞는 특정 분포를 가정하는 것입니다. 이곳에 이산형과 연속형 랜덤 변수들을 위한 몇 가지 분포들이 있습니다.

이산형 분포

• 이항 분포: 고정된 수의 독립적인 베르누이 시행에서 성공의 수를 설명합니다.
• 포아송 분포: 고정된 시간 또는 공간 간격에서 발생하는 사건의 수를 모델링합니다.

연속 분포

• 정규 분포: 평균 μ와 표준 편차 σ로 특징 짓는 종 모양의 곡선입니다.
• 지수 분포: 포아송 프로세스에서 사이의 시간을 설명합니다.

우리는 기대값, 분산 또는 다른 통계 측정을 알면 데이터 분포를 근사화할 수 있습니다. 다음 치트 시트는 연속 및 이산 랜덤 변수에 대한 몇 가지를 요약합니다.

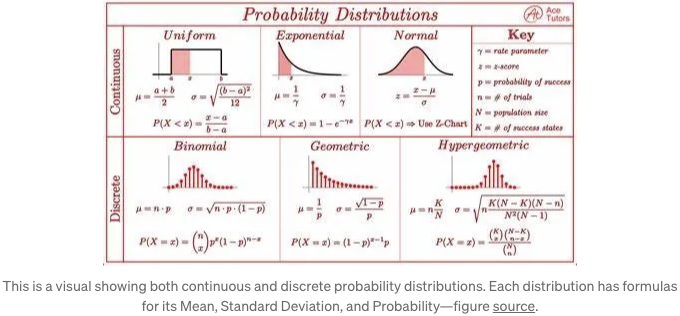
예시

정규 분포의 확률 밀도 함수를 자세히 살펴보겠습니다. 수학적으로는 다음과 같이 표현됩니다:

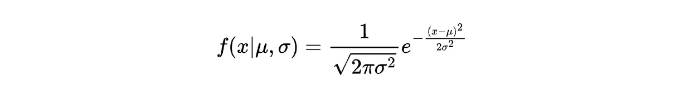
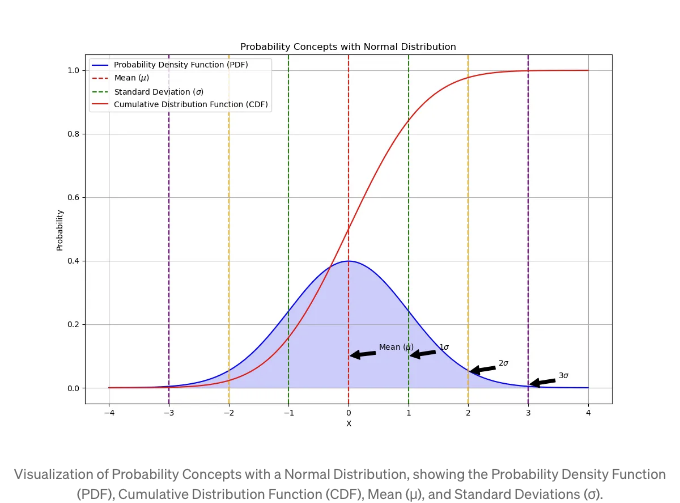
위 이미지는 정규 분포를 기반으로 한 주요 확률 개념을 시각화합니다. 그래프에는 파란색으로 표시된 확률 밀도 함수 (PDF)가 포함되어 있어 분포 내에서 다른 결과의 가능성을 나타냅니다. PDF 곡선 아래의 면적은 랜덤 변수가 특정 범위 내에 떨어질 확률을 나타냅니다.

누적 분포 함수 (CDF)는 빨간색으로 표시됩니다. 이는 0에서 시작하여 우측으로 확률을 누적하면서 1에 수렴하는 형태로 나타납니다. CDF를 사용하여 랜덤 변수가 특정 값보다 작거나 같은 확률을 결정할 수 있습니다.

수직 점선은 평균 (μ)과 평균에서의 표준 편차 (σ)를 표시합니다. 평균은 x=0에서 빨간 점선으로 표시되며, 초록색, 주황색, 보라색 점선은 각각 첫 번째, 두 번째, 세 번째 표준 편차 (±1σ, ±2σ, ±3σ)를 나타냅니다. 이러한 표준 편차는 데이터가 평균 주변에 어떻게 분포되어 있는지를 보여줍니다. 대략 68%, 95%, 99.7%가 평균에서 1σ, 2σ, 3σ 내에 각각 떨어지는 것을 보여줍니다.

도표에서 화살표는 이러한 주요 지점을 식별하는 데 도움이 되어 시각적 이해를 쉽게 만듭니다. 이 그래프는 확률의 기본 개념을 이해하려는 누구에게나 유용한 도구입니다. 특히 통계 분석의 주춧돌인 정규 분포와 다양한 머신러닝 알고리즘을 이해하는 데 도움이 됩니다.

학습을 위한 확률 활용

예를 들어, 스팸 분류할 때 𝑃(𝑌 | 𝑉𝑖𝑎𝑔𝑎𝑟𝑎, 𝑙𝑜𝑡𝑡𝑒𝑟𝑦)를 추정할 수 있습니다.

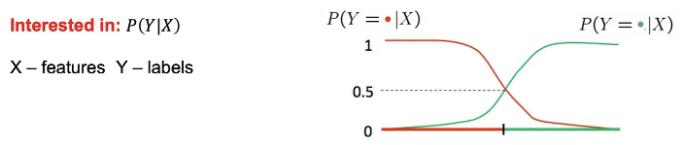
— 만약 𝑃(𝑌 | 𝑋) `0.5이면 예시를 스팸으로 분류합니다. — 그러나, 보통은 𝑃(𝑋 | 𝑌)를 모델링하는 것이 더 쉽습니다.

이것으로 우리는 최대 우도로 넘어갑니다.

최대 우도

예시: 동전 던지기

n번의 동전 던지기 결과를 이용하여 동전이 '앞'면이 나올 확률 p를 추정하고, 이 중 h개가 '앞'면으로 나온 경우의 확률을 계산합니다.

데이터의 가능성:

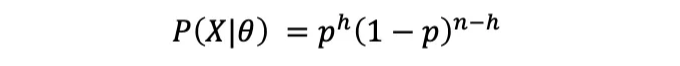
로그우도:

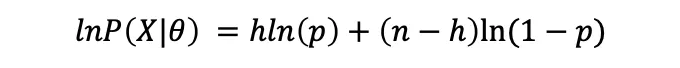
도함수를 취하고 0으로 설정하는 것:

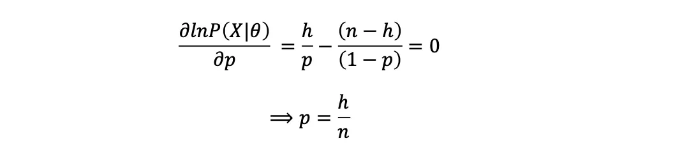
베이지안 추론

베이지안 추론은 Bayes의 정리를 사용하여 가설의 확률이 더 많은 증거가 이용 가능해질 때 업데이트되는 통계적 추론 방법입니다.

사전 확률, 가능도, 사후 확률

• 사전 ( P(H) ): 가설에 대한 초기 믿음.
• 가능도 (P(E|H) ): 가설이 주어진 경우 증거를 관측할 확률.
• 사후 ( P(H|E) ): 증거를 관측한 후에 가설에 대한 업데이트된 믿음.

Bayesian 추론의 맥락에서의 베이즈 이론:

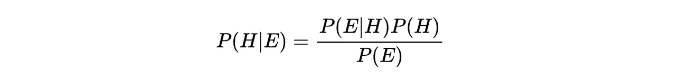
이것을 어떻게 얻었을까요? X와 Y를 사용하여 다시 생각해 봅시다.

곱셈 규칙에서

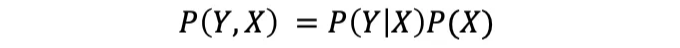
and

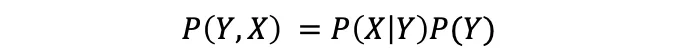
Therefore:

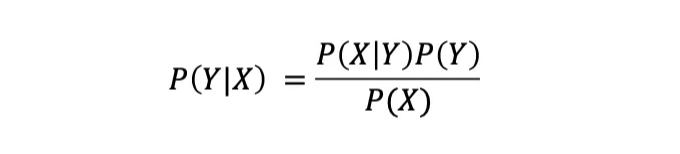
This is known as Baye's rule.

In summary:

(P(X))는 다음과 같이 계산될 수 있습니다.

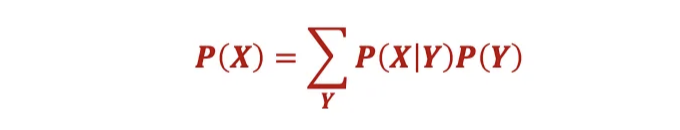
하지만 레이블을 추론하는 것은 중요하지 않습니다.

예시

드문 질환에 대해 테스트 받는 상황으로 돌아가 봅시다. 이번에는 이미 양성 판정을 받았습니다. 이제 베이즈 이론을 사용하여 이것이 진양성(True Positive)인지 확인해 보겠습니다 (즉, 테스트 결과가 사실임에도 거짓양성(False Positive)인 경우를 확인하는 것).

• 거짓양성 비율이 5%인 테스트에서 양성 판정을 받음.
• 질병이 존재할 확률은 얼마입니까?
• 100명 중 1명이 질병을 가졌다고 가정했을 때, 이것이 차이를 만들까요?
• 테스트에는 거짓음성 비율이 10%가 있습니다. 십 건 중 하나의 거짓 예측이 사실임. 이것을 활용하여 예측을 더 나아지게 할 수 있을까요?

먼저 시각적으로 살펴보겠습니다.

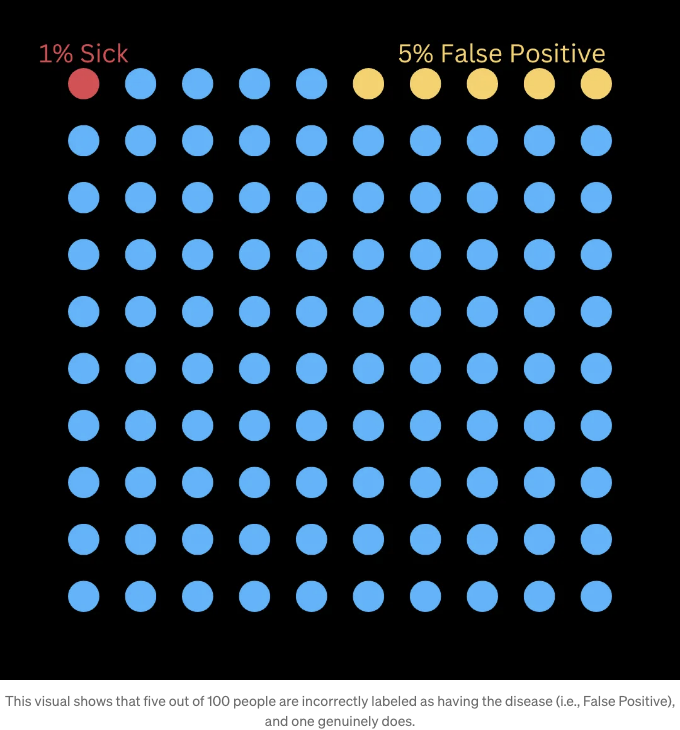
베이즈 이론을 사용해 봅시다.

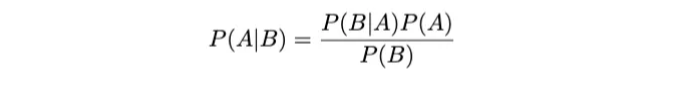
이것을 '우리가 가진 것과 원하는 것'에서 살펴보세요.

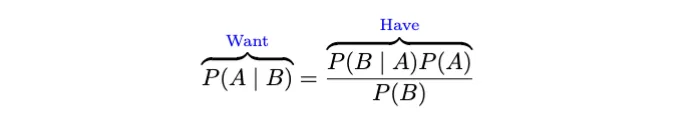
자세히 살펴보겠습니다.

따라서 사전 확률(P(B)인 분모)은 두 개의 하위 집합으로 구성되어 있으며, 이를 합집합(또는 합)으로 나타낼 수 있습니다.

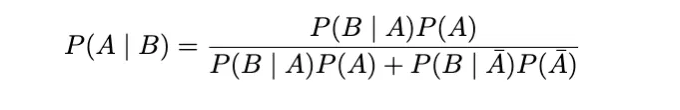
그럼, 이제 실제로 사용해 봅시다:

그러니까, 우리가 그 병을 가지고 있는 확률은 15.4% 입니다! 이는 거짓 긍정률만 고려할 때의 원본 95%보다 훨씬 좋습니다. 양성 판정을 받는 사람들의 백분율과 거짓 음성을 사용하지 않은 경우이기 때문입니다.

만약 두 번 테스트를 받아서 각각 양성 결과를 얻었다면 어떨까요? 그럴 때 병이 존재할 확률은 얼마일까요?

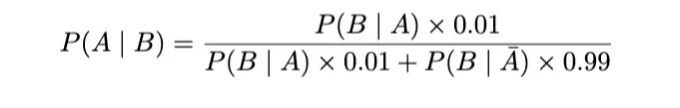
A가 질병을 가졌을 때, B가 양성 결과를 두 번 얻었을 때입니다.

두 번의 검사 후에도 여전히 원래 95%보다 낮은 확률을 가지고 있다는 것을 유의해 주세요.

이것이 베이즈의 아름다움입니다: 더 많은 지식을 습득할수록 숫자 이해력에 통합하여 확률이 어떻게 작동하는지의 정밀도를 높일 수 있습니다!

파이썬에서 확률 개념 적용하기

우리는 숫자 계산을 위해 numpy 라이브러리를 사용하고 확률 분포를 위해 scipy.stats를 사용할 것입니다.

예시: 동전 던지기 시뮬레이션

# 필요한 라이브러리 가져오기
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

# 동전 던지기 횟수
n_flips = 100
# 동전 던지기 시뮬레이션 (앞면은 1, 뒷면은 0)
coin_flips = np.random.binomial(1, 0.5, n_flips)

# 앞면의 개수 세기
n_heads = np.sum(coin_flips)
print(f"앞면의 개수: {n_heads}")
# 앞면의 확률 계산
p_heads = n_heads / n_flips
print(f"앞면의 추정 확률: {p_heads:.2f}")

확률 분포 시각화

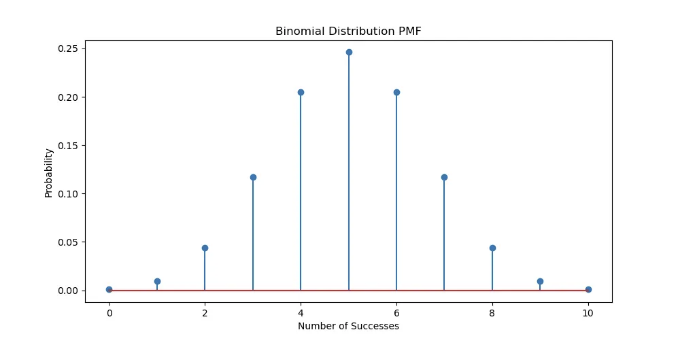
# 이항 분포 그래프 그리기
n_trials = 10
p_success = 0.5
x = np.arange(0, n_trials+1)
binomial_pmf = stats.binom.pmf(x, n_trials, p_success)

plt.figure(figsize=(10, 5))
plt.stem(x, binomial_pmf)
plt.title('이항 분포 PMF')
plt.xlabel('성공 횟수')
plt.ylabel('확률')
plt.show()

생성됨:

Toy Example: Bayesian Inference for Coin Flipping

We’ll use Bayesian inference to estimate the probability of heads for a biased coin.

Prior Belief

베타 사전 분포를 가정하고, 파라미터 α = 2, β = 2를 사용하여 균일한 사전 믿음을 표현합니다.

# 사전 분포 정의
alpha_prior = 2
beta_prior = 2
prior = stats.beta(alpha_prior, beta_prior)

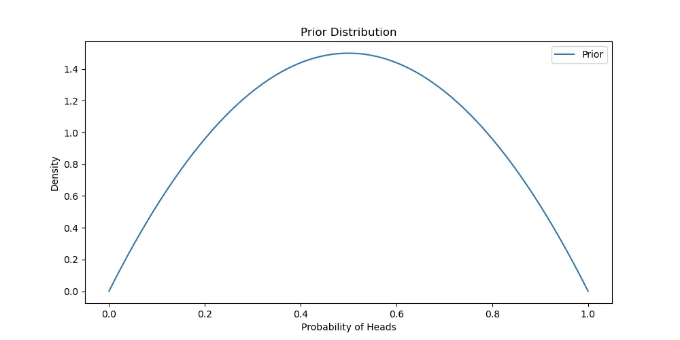
# 사전 분포 그래프
x = np.linspace(0, 1, 100)
plt.figure(figsize=(10, 5))
plt.plot(x, prior.pdf(x), label='사전')
plt.title('사전 분포')
plt.xlabel('앞면 확률')
plt.ylabel('밀도')
plt.legend()
plt.show()

생성된 그림은 아래와 같습니다:

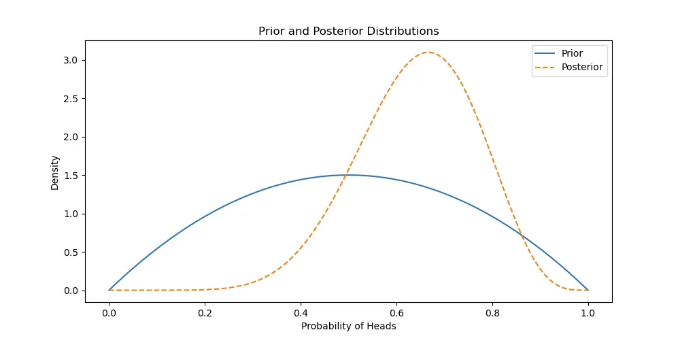
가능성과 사후확률

관측된 데이터(증거)로 사전 확률을 업데이트하여 사후 분포를 얻습니다.

# 관측된 앞면과 뒷면의 수
n_heads = 7
n_tails = 3

# 사후 분포를 업데이트합니다
alpha_posterior = alpha_prior + n_heads
beta_posterior = beta_prior + n_tails
posterior = stats.beta(alpha_posterior, beta_posterior)

# 사후 분포를 그래픽으로 표시합니다
plt.figure(figsize=(10, 5))
plt.plot(x, prior.pdf(x), label='사전분포')
plt.plot(x, posterior.pdf(x), label='사후분포', linestyle='--')
plt.title('사전 및 사후 분포')
plt.xlabel('앞면이 나올 확률')
plt.ylabel('밀도')
plt.legend()
plt.show()

생성됨:

결론

확률 이론은 많은 통계 및 머신러닝 기술을 기반으로 하는 기본적인 데이터 과학 구성 요소입니다. 이 튜토리얼에서는 기본적인 정의부터 고급 베이지안 추론에 이르기까지 확률에 대한 필수 개념을 실용적인 예제와 파이썬 구현으로 다루었습니다. 이러한 개념을 정복함으로써 더 견고한 모델을 구축하고, 더 나은 결정을 내리며, 데이터에서 더 깊은 통찰력을 얻을 수 있습니다.

다양한 확률 분포, 가설 및 데이터 집합을 실험하여 데이터 과학 프로젝트에서의 확률 이론의 다양한 응용을 탐색해보세요.

이 시리즈의 이전 부분인 데이터 과학자를 위한 미적분 및 선형 대수에 관한 내용도 확인해보세요:

행동 요령

이 블로그가 여러분이 기계 학습에서 수학의 중요성을 이해하는 데 도움이 되었기를 바라요.

만약 이 콘텐츠를 즐겼다면, 저희 뉴스레터를 구독하여 앞으로의 게시물을 확인해보세요. 여러분의 피드백을 소중히 생각하며 여러분의 생각, 질문, 제안을 댓글로 남기도록 장려합니다. 함께 도움이 될 수 있는 동료나 동료들과 이 블로그를 공유하는 것을 잊지 마세요.

드. 로빈슨 박사를 팔로우하려면 Medium, LinkedIn 및 Facebook을 방문해 주세요. 논문, 블로그, 이메일 수신 동의 등을 위한 홈페이지도 방문해 주세요!