이전 글에서는 Python으로 이산 푸리에 변환(DFT)을 구현했습니다.

DFT 알고리즘을 통해 우리는 시끄러운 신호에서 숨겨진 패턴을 찾기 위한 도구를 얻었습니다. 시간 값의 벡터를 주파수 값의 벡터로 선형 변환함으로써 이전 신호를 구성하는 사인파 파형의 진폭, 주파수 및 위상을 드러냅니다.

이번 글에서는 그 반대 과정을 살펴보겠습니다: 주파수 값의 벡터를 시간 값의 벡터로 변환하는 것입니다.

수학적으로, 역 이산 푸리에 변환(iDFT)은 다음과 같습니다:

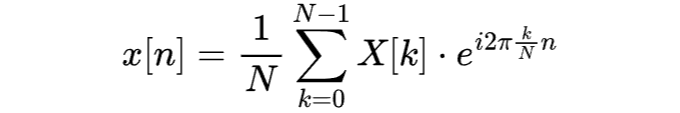
iDFT Formula

여기서,

N은 샘플 수입니다.
n은 현재 샘플입니다.
k는 현재 주파수입니다.
X[k]는 n에서의 DFT입니다.
x[n]은 n에서의 iDFT입니다.

이 역과정은 이산 푸리에 변환 행렬이 정방행렬이며 역행렬이 가능하기 때문에 가능합니다(이전 글에서 본 지수값 행렬을 상기해보세요). 이상적으로는 우리가 원래의 소음이 섞인 신호를 되찾을 수 있어야 합니다.

그럼 코딩을 시작해봅시다!

파이썬 코드

DFT 함수는 각 주파수에서의 진폭과 위상을 포함한 복소수 벡터를 반환했습니다. 우리는 그 벡터를 X_k라고 부르기로 했습니다.

이제 X_k를 사용하여 원본 신호를 복원할 것입니다.

def iDFT(X_k):
    N = X_k.size
    n = np.arange(N)
    k = n.reshape((N,1))

    e = np.exp(2j * np.pi * k * n / N)
    x = np.zeros_like(X_k)
    for row in range(N):
        for col in range(N):
            x[row] += e[row, col] * X_k[col]
    x /= N

    return x.real

여기서 주목해야 할 중요한 점들:

DFT 함수에서 X_k를 선언할 때 데이터 유형을 명시적으로 정의했었습니다.

X_k = np.zeros_like(k, dtype=np.complex128)

하지만 여기서 x를 선언할 때는 데이터 유형을 명시하지 않아도 됩니다. 실제 수학 연산이 복소수를 포함하더라도 데이터 유형을 명시할 필요가 없는 이유는 무엇일까요?

zeros_like 함수가 작동하는 방식 때문입니다. 이 함수는 입력 인수의 모양뿐만 아니라 데이터 유형도 복사합니다. X_k의 경우, k는 실수 벡터였습니다. X_k는 복소수 연산과 관련이 있으므로 그 데이터 유형을 복소수로 명시적으로 정의해 주어야 했습니다.

이 경우 X_k는 이미 복소수입니다. 이를 zeros_like의 인수로 전달하면 x도 복소수 벡터가 됩니다.

신호를 플롯할 때, 복소수 값의 실부분에만 관심이 있습니다. 그래서 x 대신 x.real이 반환됩니다.

이것이 진폭 스펙트럼입니다:

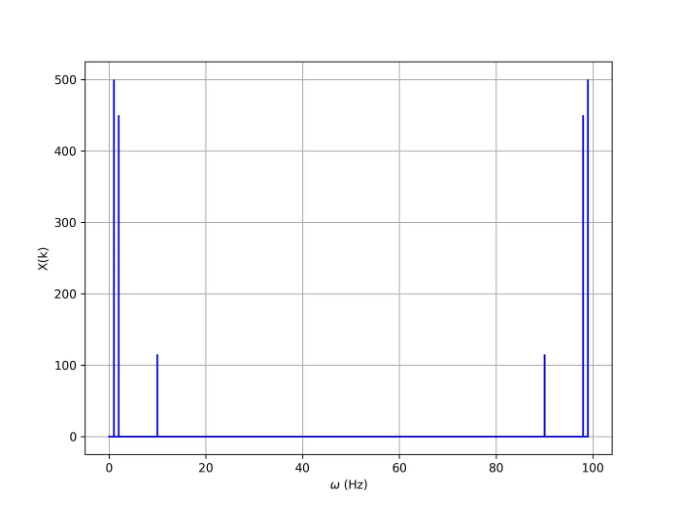
Amplitude Spectrum

iDFT 함수를 사용하여 신호를 재구성하고 원래 신호와 비교해 보겠습니다.

inv_x = iDFT(X_k);

plt.figure((figsize = (14, 5)));
plt.subplot(121);
plt.plot(t, x, "b");
plt.xlabel("t");
plt.ylabel("x");
plt.title("Original Signal");
plt.grid(True);
plt.subplot(122);
plt.plot(t, inv_x, "r");
plt.xlabel("t");
plt.ylabel("x");
plt.title("Reconstructed Signal");
plt.tight_layout();
plt.grid(True);

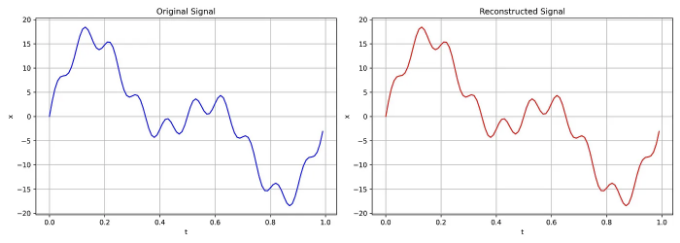
Reconstructed Signal

그런데 부활이 정말 잘 되었네요!

물론 첫 번째에 깨끗한 신호가 있었기 때문에 부활 프로세스가 쉬워졌습니다.

하지만 이 프로세스는 실제 신호에서도 효율적입니다. 시간 및 주파수 도메인 간에 DFT 행렬만 사용하여 전환할 수 있는 방법이 명확히 이해되었으면 좋겠습니다.

벡터화

이전에 말한 대로 for 루프는 느립니다. 그래서 iDFT 함수를 벡터화해 봅시다.

def viDFT(X_k):
    N = X_k.size
    n = np.arange(N)
    k = n.reshape((N,1))

    e = np.exp(2j * np.pi * k * n / N)
    x = np.dot(e, X_k) / N

    return x.real

2개 함수에 의해 소요된 시간을 비교해 봅시다.

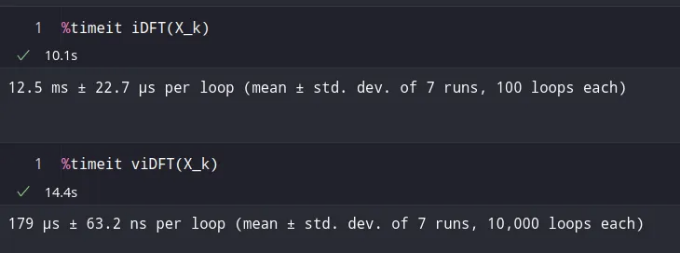
이전과 마찬가지로, 벡터화된 함수가 10⁴배 빠릅니다.

이전 글을 이어서, 이제 Python에서 역 이산 푸리에 변환을 구현했습니다.

다음 기사에서는 DFT 알고리즘을 크게 가속화하는 알고리즘에 대해 논의해봅시다.

하디크 메디 궁금증을 유지하세요

파이썬으로 역 이산 푸리에 변환 구현하기

파이썬 코드

벡터화